
As we will see, these two types of reflections are simple to understand visually, and have a similarly straightforward algebraic interpretation.ĭefinition: Reflecting a Function in the Horizontal or Vertical AxisĬonsider a function 𝑦 = 𝑓 ( 𝑥 ) that is plotted on the standard 𝑥 𝑦-axis.
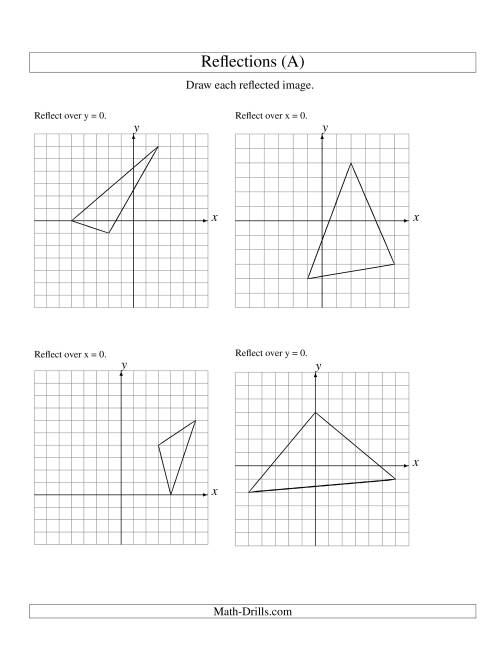
These can all be understood algebraically as well as visually, although the simplest case is the reflection in either of the axes. It is possible to reflect any function through any straight line, such as the line 𝑦 = 𝑥 or any other of the form 𝑦 = 𝑚 𝑥 + 𝑏.

This explainer will focus on what happens to a graph when it is reflected in the 𝑥-axis or 𝑦-axis. Fortunately, many transformations are simple to explain using intuitive algebraic rules, especially for some types of translations, reflections, and dilations. Given that a function is ideally written as a formula or an algebraic expression, it is a natural extension to ask how transforming the function can be represented within this framework. If a function is well-defined (either algebraically or with a suitably descriptive graph), then its qualitative behavior can be known at all points, and we might then be interested in how the function behaves when it is subjected to various transformations. In many senses, understanding the effects of transformation on a function can be thought of as a generalization of the above approach. Approaching the topic in such a way will allow for a visual understanding of transformations to be combined with concepts that are drawn from coordinate geometry. A common way of illustrating this is to refer to the vertices of a shape, which can be expressed using precise coordinates and hence can have these movements tracked as the result of transformations being applied. Once these notions are understood intuitively, it is common to begin treating the subject a little more precisely, with the aim of understanding exactly what happens to a shape when it undergoes some combination of transformations. Often, these concepts are illustrated using polygons and other common concepts, usually with familiar and ubiquitous shapes, such as triangles and circles. One of the fundamental concepts in geometry is that of transforming a shape with the standard actions of translation, rotation, reflection, and dilation.
REFLECTION ON Y AXIS FUNCTION HOW TO
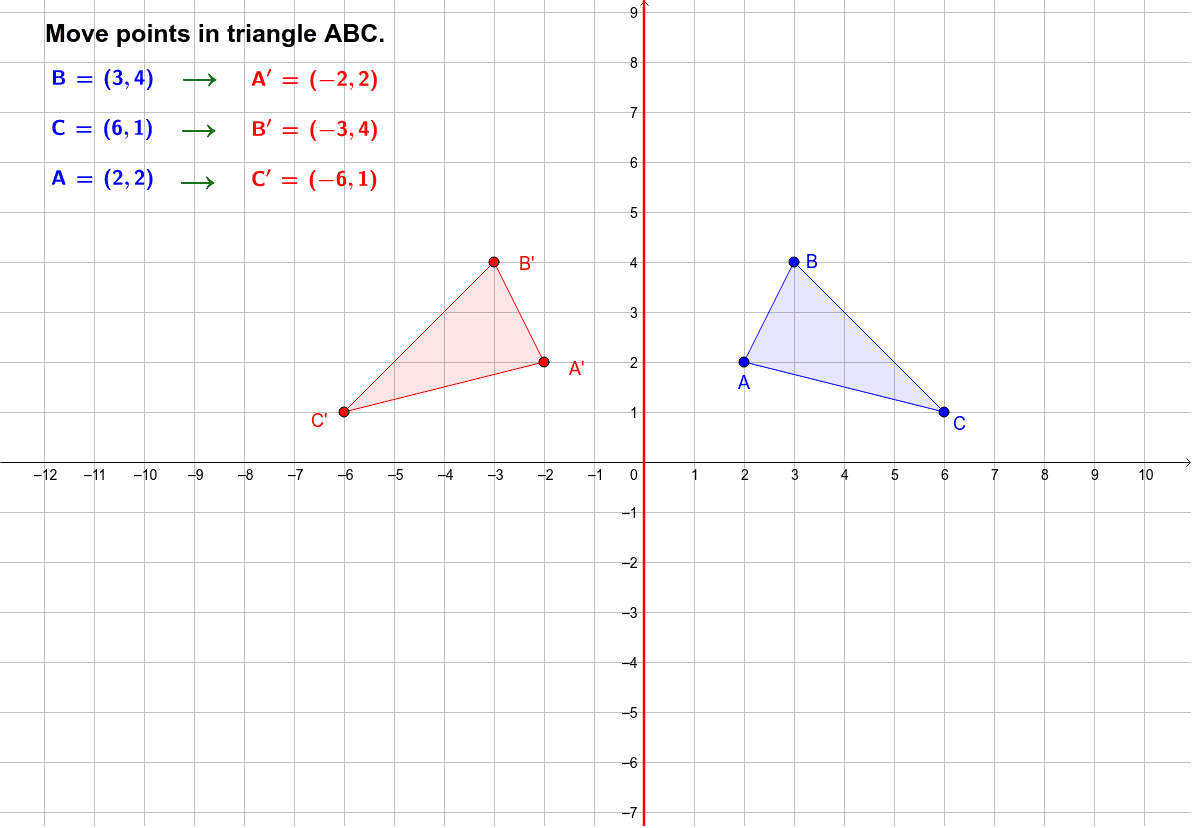
Images/mathematical drawings are created with GeoGebra.In this explainer, we will learn how to reflect a graph on the 𝑥- or 𝑦-axis, both graphically and algebraically. When the square is reflected over the line of reflection $y =x$, what are the vertices of the new square?Ī. Suppose that the point $(-4, -5)$ is reflected over the line of reflection $y =x$, what is the resulting image’s new coordinate?Ģ.The square $ABCD$ has the following vertices: $A=(2, 0)$, $B=(2,-2)$, $C=(4, -2)$, and $D=(4, 0)$.
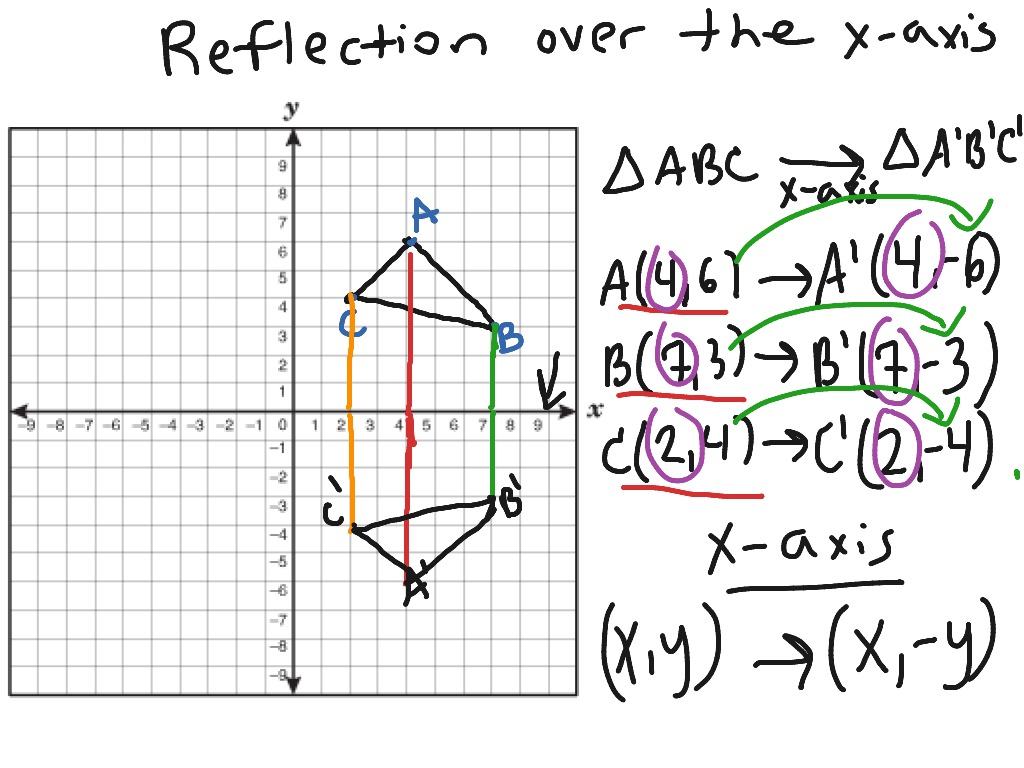
Use the coordinates to graph each square - the image is going to look like the pre-image but flipped over the diagonal (or $y = x$). Plot these three points then connect them to form the image of $\Delta A^ Read more Halfplane: Definition, Detailed Examples, and Meaning


 0 kommentar(er)
0 kommentar(er)
